介绍
图搜索算法中最常见的一个应用就是路径规划,常见的针对无权图的搜索有DFS和BFS,引入权重后,Dijkstra算法解决了单源最短路径问题,而启发式搜索的存在(GBFS,A*)则能够通过启发函数来提高搜索效率。
DFS
深度优先搜索(Depth First Search)通过维护栈这一数据结构,能够实现对全部路径的搜索,但他会沿着一条路走到最后,在没有结果时才会回头选择另一条路,因此无法保证找到的路径是最优路径。
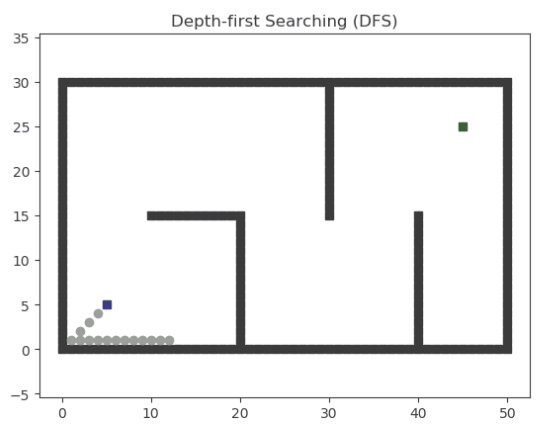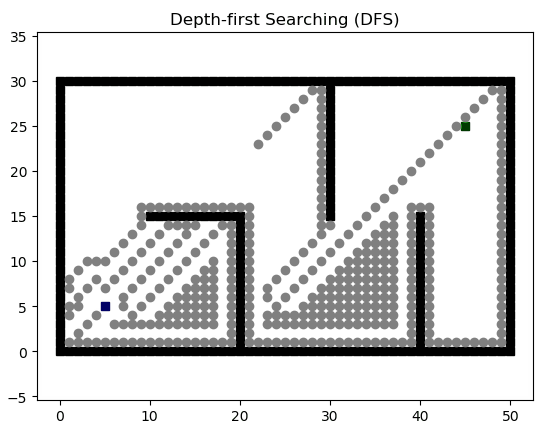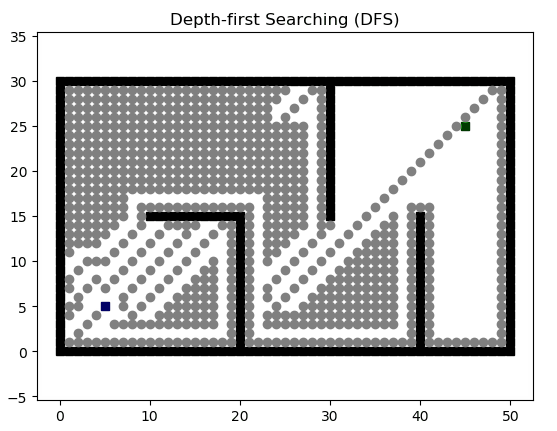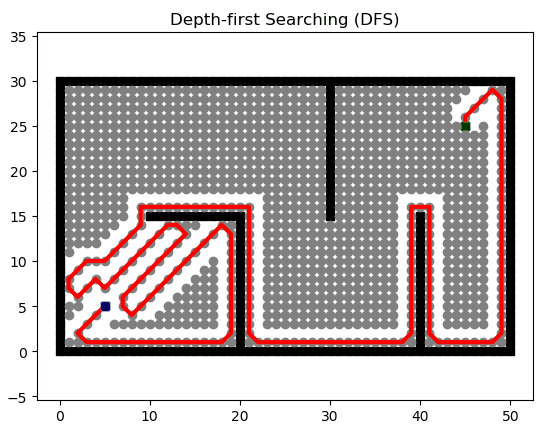
def dfs(start_point, goal_point):
path = []
seen = set()
stack = []
seen.add(start_point)
stack.append(goal_point)
while len(stack) > 0:
current = stack.pop()
path.append(current)
if current == goal_point:
break
if not graph.neighbors(current):
path.pop()
continue
for next in graph.neighbors(current):
if next not in seen:
stack.append(next)
seen.add(next)
return path
BFS
广度优先搜索(Breadth First Search)在搜索无权图最短路径时很有用,他会优先探索当前位置的所有方向而不是向着一个方向探索到最后,这也是广度的由来。实现BFS通常依靠队列。同时,我们通过字典来保存我们走过的路径,并通过从终点开始的反向遍历得到路径。
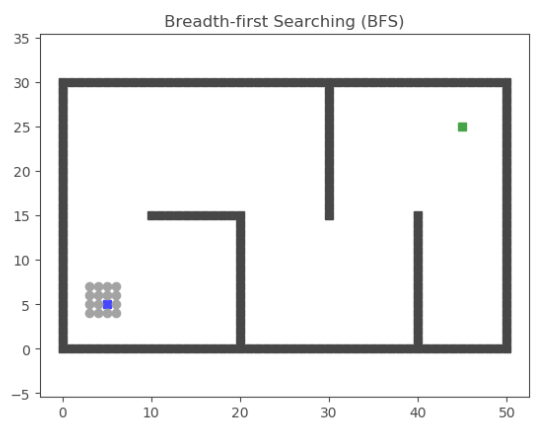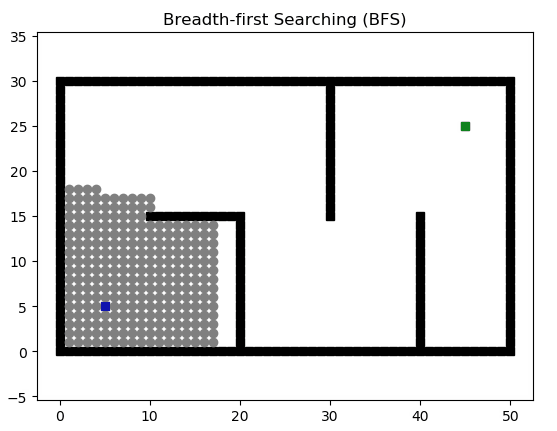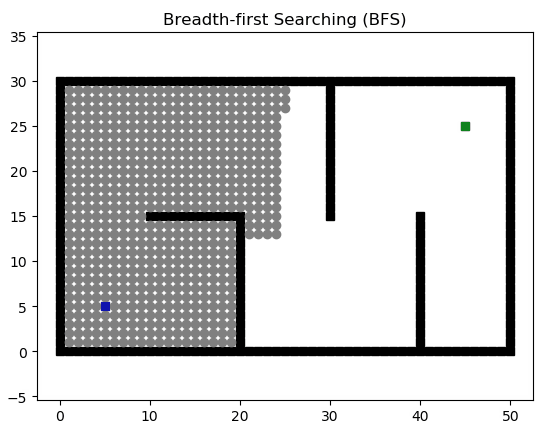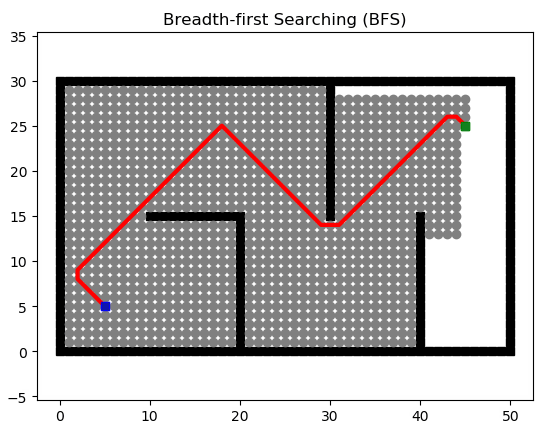
def bfs(start_point, goal_point):
frontier = Queue()
frontier.put(start_point)
came_from = dict()
came_from[start_point] = None
seen = set()
seen.add(start_point)
while not frontier.empty():
current = frontier.get()
if current == goal_point:
break
for next in graph.neighbors(current):
if next not in seen:
frontier.put(next)
seen.add(next)
came_from[next] = current
path = []
goal = goal_point
path.append(goal)
while came_from[goal]:
goal = came_from[goal]
path.append(goal)
path.reverse()
return path
Dijkstra
权重的概念引入后,我们不再寻找最短路径,而是寻找权重花费最小的路径。
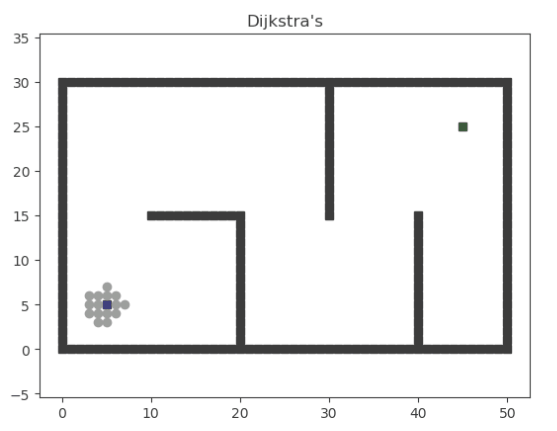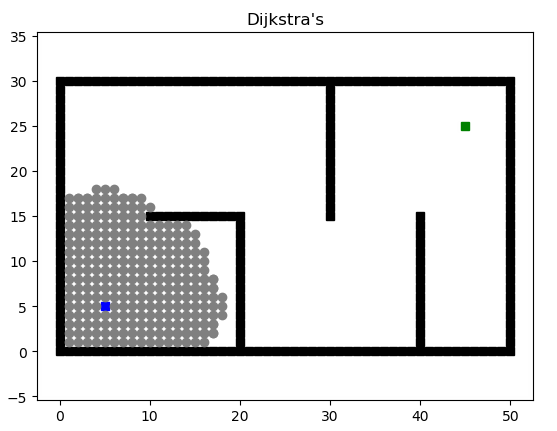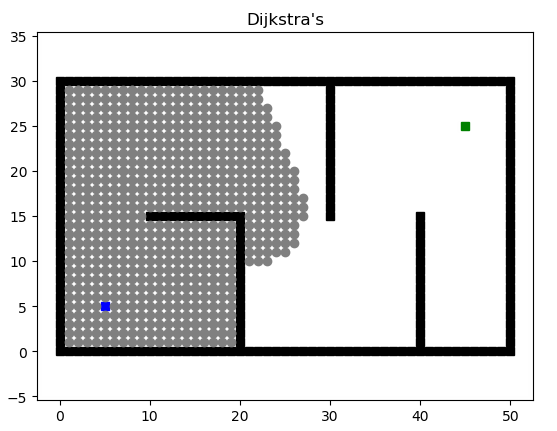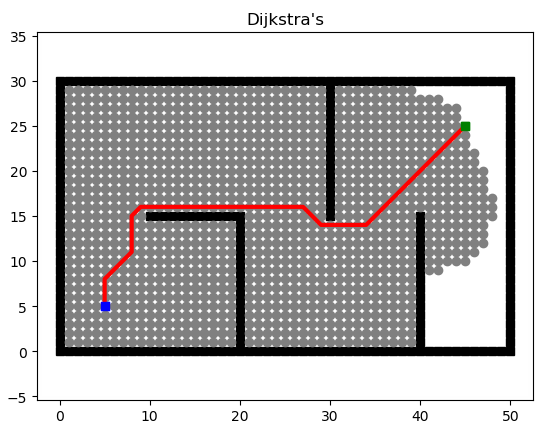
def dijkstra(start_point, goal_point):
frontier = PriorityQueue()
frontier.put((0, start_point))
came_from = dict()
came_from[start_point] = None
cost_so_far = dict()
cost_so_far[start_point] = 0
seen = set()
seen.add(start_point)
while not frontier.empty():
current = frontier.get()[1]
if current == point:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in seen or new_cost < cost_so_far[current]:
cost_so_far[next] = new_cost
priority = new_cost
frontier.put((priority, next))
seen.add(next)
came_from[next] = current
path = []
goal = goal_point
path.append(goal)
while came_from[goal]:
goal = came_from[goal]
path.append(goal)
path.reverse()
return path
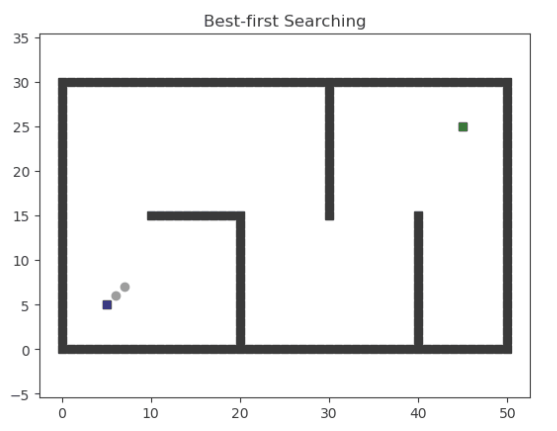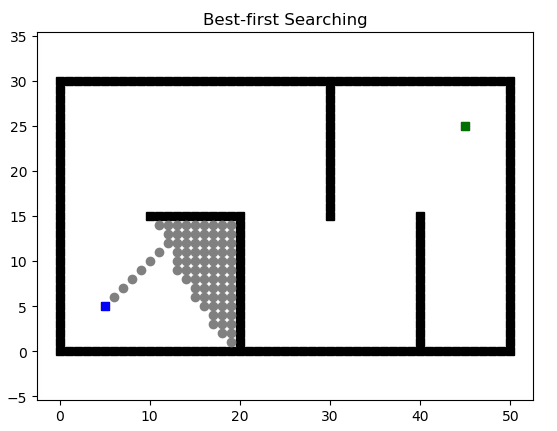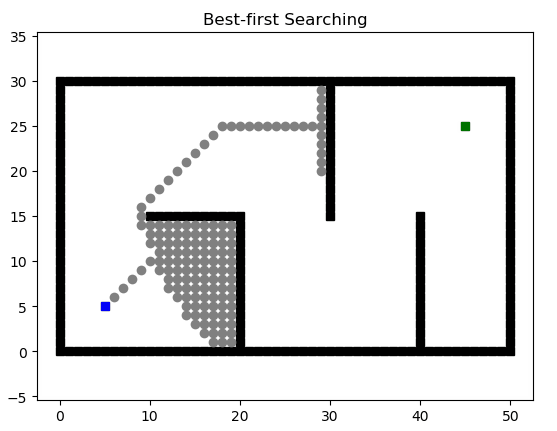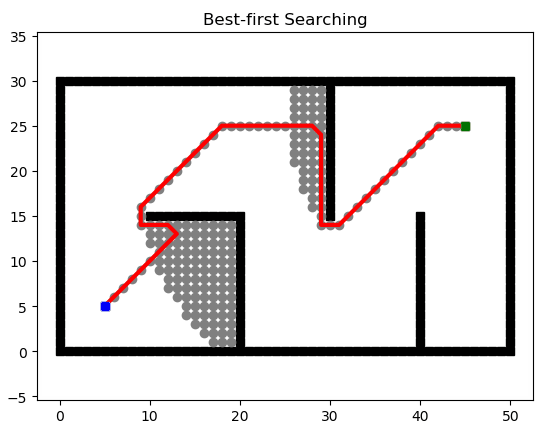
GBFS
贪婪最佳优先算法(Greedy Best First Search),相对于BFS算法,有了启发性,即他不是每一次都向全部方向进行搜索,而是通过启发优先决定朝哪个方向进行寻找,我们可以认为他是“有目的”。
def heuristic(a, b):
return abs(a.x - b.x) + abs(a.y - b.y)
def gbfs(start_point, goal_point):
frontier = PriorityQueue()
frontier.put((0, start_point))
came_from = dict()
came_from[start_point] = None
seen = set()
seen.add(start_point)
while not frontier.empty():
current = frontier.get()
if current == goal_point:
break
for next in graph.neighbors(current):
if next not in seen:
priority = heuristic(goal_point, next)
frontier.put((priority, next))
seen.add(next)
came_from[next] = current
path = []
goal = goal_point
path.append(goal)
while came_from[goal]:
goal = came_from[goal]
path.append(goal)
path.reverse()
return path
A*
GBFS的缺点也很明显,他未必能找到真正短的路径(见#解读),而我们想要获得Dijkstra和GBFS两种算法的优点,于是A*算法应运而生,A*算法使用两个函数值(权重最小和距离最短)来决定他的路径规划。
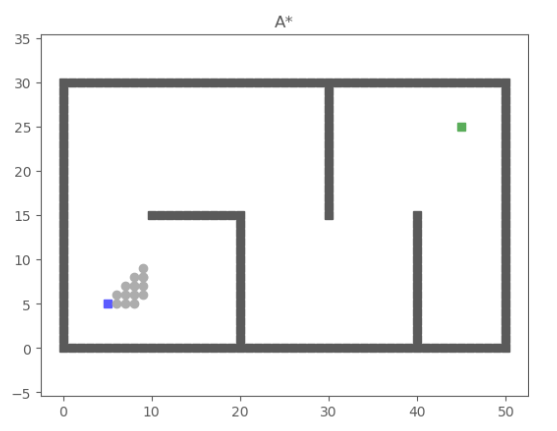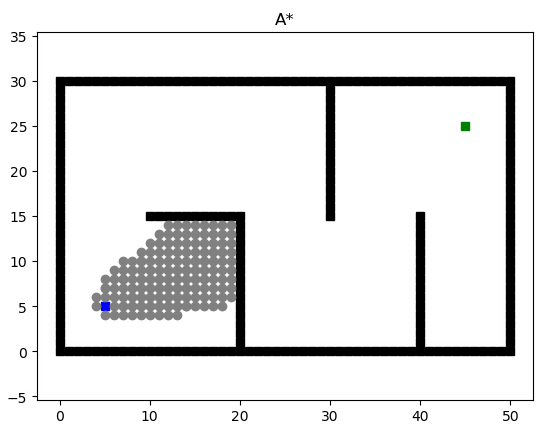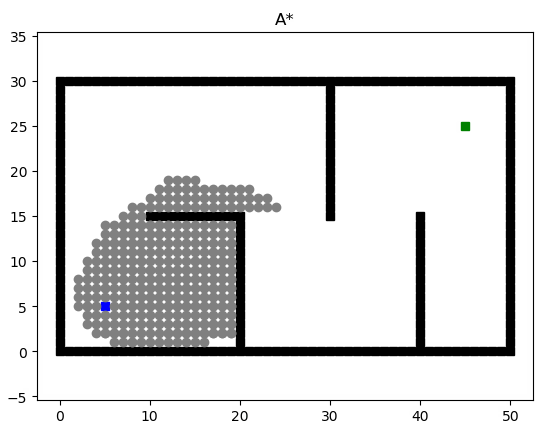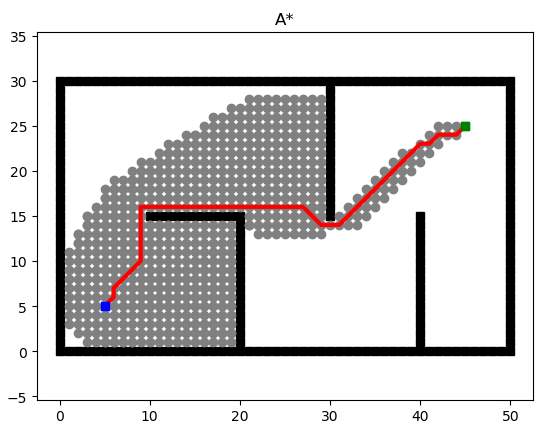
def heuristic(a, b):
return abs(a.x - b.x) + abs(a.y - b.y)
def Astar(start_point, goal_point):
frontier = PriorityQueue()
frontier.put((0, start_point))
came_from = dict()
came_from[start_point] = None
cost_so_far = dict()
cost_so_far[start_point] = 0
seen = set()
seen.add(start_point)
while not frontier.empty():
current = frontier.get()[1]
if current == point:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in seen or new_cost < cost_so_far[current]:
cost_so_far[next] = new_cost
priority = new_cost + heuristic(goal_point, next)
frontier.put((priority, next))
seen.add(next)
came_from[next] = current
path = []
goal = goal_point
path.append(goal)
while came_from[goal]:
goal = came_from[goal]
path.append(goal)
path.reverse()
return path
三种权重搜索算法比较