介绍
Dijkstra算法解决的是带权重的有向图上单源最短路径问题,该算法要求所有边的权重都为非负值。
算法主要通过维护结点集合S。通过从结点集V-S中选择最短路径最小的结点u,将其加入进S中,并对所有从u发出可到达V-S集合中结点的边进行松弛操作。
对邻接表进行操作
松弛操作:对于一条从 顶点u指向 顶点v的边 u–>v来说,如果满足 d[u]+w(u,v)<d[v],就更新 d[v],使得 d[v]=d[u]+w(u,v);这就是对 边uv的一次松弛操作;
其中,w(u,v)表示边的权重,d(u)表示顶点u到达源s的最短距离(目前已知)
因此我们可以将算法理解为三个操作:
- 找到V-S集合中距离S集合最小结点
- 将结点加入S集合中
- 对V-S中剩余结点进行松弛操作。
算法描述
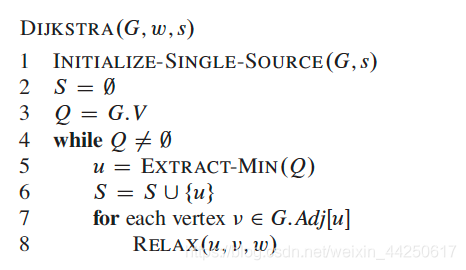
解释
算法的主要逻辑为while循环。Q始终为Q=V-S。每一次通过EXTRACT-MIN(Q)取出Q中距离最小值u。并将u放入S集合中。之后在for循环中对Q中剩余结点进行松弛操作。
对距离进行更新。
分析
算法通过每次从Q中找出距离最小的一个结点插入到S中,并将Q中剩余的结点距离进行松弛,直到Q中没有结点结束。因为Q中初始结点一共有V个,因此一定会有一次O(V)操作(全部插入)。
注意到我们每次只需要松弛刚插入结点连接到的表,由于采用邻接表操作,我们对每一个边只会松弛一次,因此一共会执行|E|次。
找到最小结点的操作可以有多种方式实现,下面介绍三种。
利用一次遍历实现(常通过维护数组)
我们每一次都通过遍历Q中全部结点找到最小值,这时候需要对一次插入结点都需要执行一个O(V)操作。算法的时间复杂度为
$$ O(V^2 + E) = O(V^2) $$
利用二叉堆实现
显然,如果我们每一次都要找到最小值,可以通过使用二叉堆实现优先队列来优化寻找最小值的算法。这样我们可以将查找最小值的操作优化到O(lgV)
而对于二叉堆,每一次修改距离并加入到二叉堆都需要一次更新,因此复杂了松弛操作,时间复杂度为
$$ O((V+E)lgV) $$
即每一次删除Q中一个结点和将结点距离松弛化都需要lgV时间
因此,是否优于第一种需要考虑E的范围,即图是稀疏图还是稠密图
利用斐波那契堆
斐波那契堆的对于找到最小值并进行删除需要的时间与二叉堆一样,都是O(lgV),但对松弛操作,斐波那契堆的摊还代价是O(1),因此可以实现更好的优化,他的时间复杂度为
$$
O(VlgV + E)
$$